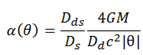
A point-mass lens and a point-mass source
In the specific case of a point-mass lens and a point-mass source the deflection angle is
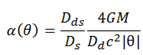
and the deflection potential
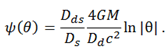
With these we get that the lens equation is
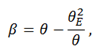
where we have used the Einstein’s angle
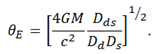
In this case there are always two point-images,
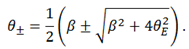
Using the deflection potential we get that there is only a critical curve, a ring with θ=θE. The corresponding caustic is point-like, located in β=0. The magnification of each image is
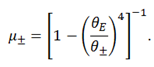
Although the magnification is the brightness of each image, in this case it appears as the size of the image. That is done to emphasize the fact that when the source is very far from the lens (in the plane of the sky) the observer only sees one image with the same shape and size of the source, because the other has zero brightness. When the source is on the caustic, the images are infinitely magnified, so in this case we see that they get really big.
We have taken G/c2=1 and 1 light-year=1. As the angles are really small we multiply them by 107, which simulates the effect of looking through a telescope.